¿Qué es el teorema de Pitágoras y cómo se aplica?

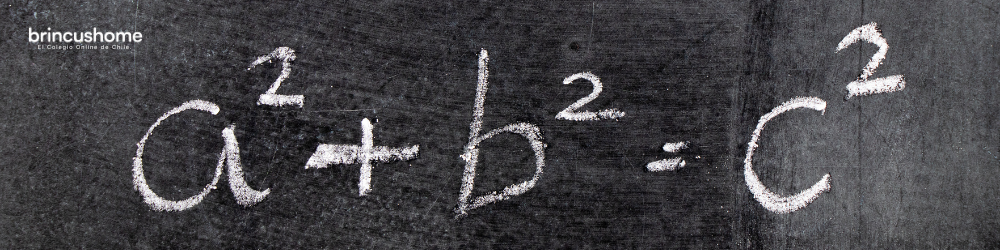
El Teorema de Pitágoras es una de las piedras angulares de la geometría y una herramienta esencial que todos debemos conocer. Este principio, aplicable únicamente en triángulos rectángulos, tiene múltiples usos en situaciones cotidianas, desde medir distancias hasta resolver problemas prácticos en el hogar. Si alguna vez te preguntaste cómo calcular la hipotenusa de un triángulo o verificar si es rectángulo, aquí encontrarás todas las respuestas.

¿Qué dice el Teorema de Pitágoras?

En un triángulo rectángulo, el cuadrado de la longitud de la hipotenusa (el lado más largo) es igual a la suma de los cuadrados de las longitudes de los dos catetos (los lados que forman el ángulo recto). Matemáticamente, se expresa como: c^2=a^2+b^2

Dónde:

1. c: Es la longitud de la hipotenusa.
2. a y b: Son las longitudes de los catetos.

¡Hay que tener mucho cuidado con que el triángulo sí o sí sea rectángulo o sino no podremos aplicar este teorema!

Un ejemplo lo podemos ver en el siguiente triángulo rectángulo:

Aquí la hipotenusa es el lado más largo y que está frente al ángulo recto (90°) por lo que su longitud es 5. Los catetos tiene longitud 3 y 4 y vemos que se cumple la igualdad:

5^2=3^2+4^2

5∙5=3∙3+4∙4

25=9+16

25=25

Como se cumple, podemos afirmar que el triángulo es rectángulo en C.

El teorema se puede utilizar para:

1. Calcular la hipotenusa: Si conoces las longitudes de los dos catetos ( y ), puedes encontrar el valor de :

Si usamos el mismo ejemplo anterior, tenemos:

En este paso podemos aplicar la raíz cuadrada a ambos lados de la ecuación:

√(c^2 )=√25

Como la raíz cuadrada de un número al cuadrado es el valor absoluto del número (¡Puedes ir a ver la publicación del blog que nos habla de valor absoluto para más información 😉!) tenemos:

√(c^2 )=√25

|c|=5

Los números cuyo valor absoluto es igual a 5 es el 5 y el -5. Como en este contexto estamos hablando de distancias, nos quedaremos solo con el 5 positivo!

|c|=5

c=5

Por lo tanto la hipotenusa tiene un valor de c=5.

En un futuro no será necesario que realices todas estas operaciones, pero si es muy importante que entiendas de dónde viene el resultado.

1. Calcular un cateto: Si conoces la hipotenusa () y un cateto ( o ), puedes encontrar el otro cateto:

Si usamos el mismo ejemplo anterior, y asumimos que tenemos la medida del cateto a:

1. Verificar si un triángulo es rectángulo: Si los lados , y de cualquier triángulo cumplen la relación , entonces el triángulo es rectángulo.

Los números que cumplen con el Teorema de Pitágoras se llaman Tríos Pitagóricos. Es decir, un trío pitagórico es un conjunto de tres números enteros positivos que cumplen con el Teorema de Pitágoras. En estos tríos, a y b son los catetos, y c es la hipotenusa. Los tríos pitagóricos representan las longitudes de los lados de un triángulo rectángulo.

Algunos tríos pitagóricos más usados son los siguientes:

Además, si (a,b,c) es un trío pitagórico y lo multiplicamos por cualquier número positivo, el resultado también es un trío pitagórico .

Por ejemplo, el trío (3,4,5) si lo multiplicamos por 2 resulta (6,8,10) y este ¡también es un trío pitagórico!

Por último, veamos cómo usamos el Teorema de Pitágoras para calcular la diagonal de un cuadrado.

Si tenemos un cuadrado de lado 4 podemos aplicar el Teorema de Pitágoras porque al trazar su diagonal se forman 2 triángulos rectángulos, como vemos en la imagen. Si aplicamos el Teorema de Pitágoras a cualquiera de los dos triángulos tenemos lo siguiente:

Por lo tanto, la diagonal del cuadrado de lado 4 mide √32.

Conclusión

El Teorema de Pitágoras es una herramienta poderosa que no solo tiene aplicaciones en el aula, sino también en la vida diaria. Desde resolver problemas geométricos hasta realizar mediciones prácticas, este principio es fundamental para entender y manejar el mundo que nos rodea. ¡Prueba aplicarlo en tus proyectos y observa su utilidad!